

时间: 2024-12-16 13:17:02 | 作者: 扑克王app客服
当输入电压处于交流电压的正半周时,二极管导通,输出电压vo=vi-vd。当输入电压处于交流电压的负半周时,二极管截止,输出电压vo=0。半波
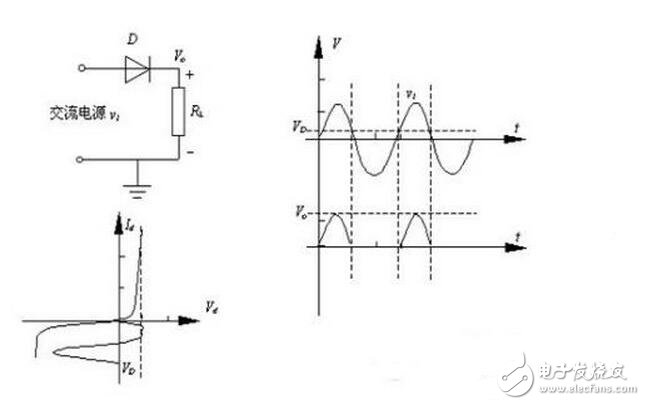
对于使用直流电源的电动机等功率型的电气设备,半波整流输出的脉动电压就足够了。但对于电子电路,这种电压则不能直接作为半导体器件的电源,还一定要经过平滑(滤波)处理。平滑处理电路实际上就是在半波整流的输出端接一个电容,在交流电压正半周时,交流电源在通过二极管向负载提供电源的同时对电容充电,在交流电压负半周时,电容通过负载电阻放电。
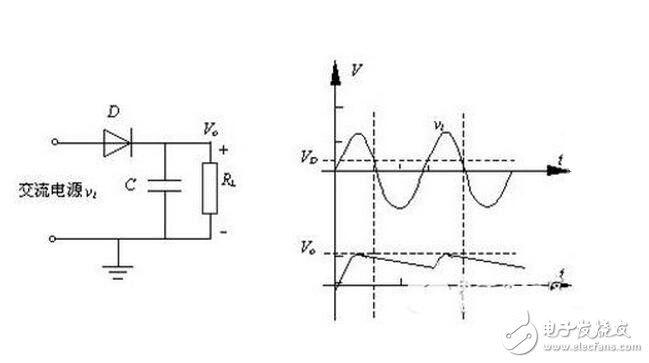
(3)电容输出半波整流电路中,二极管承担最大反向电压为2倍交流峰值电压(电容输出时电压叠加)。
(3)实际电路中,半波整流电路二极管和电容的选择一定要满足负载对电流的要求。
当输入电压处于交流电压的正半周时,二极管D1导通,输出电压Vo=vi-VD1。当输入电压处于交流电压的负半周时,二极管D2导通,输出电压Vo=vi-VD2。
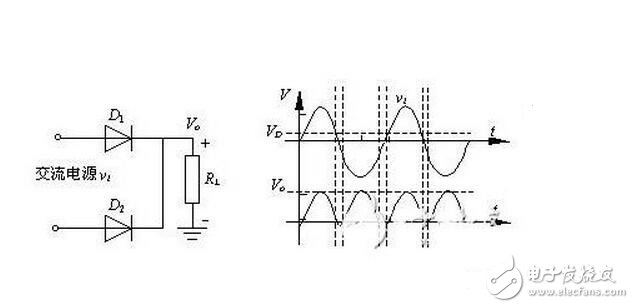
由上述分析可知,二极管全波整流电路输出的仍然是一个方向不变的脉动电压,但脉动频率是半波整流的一倍。
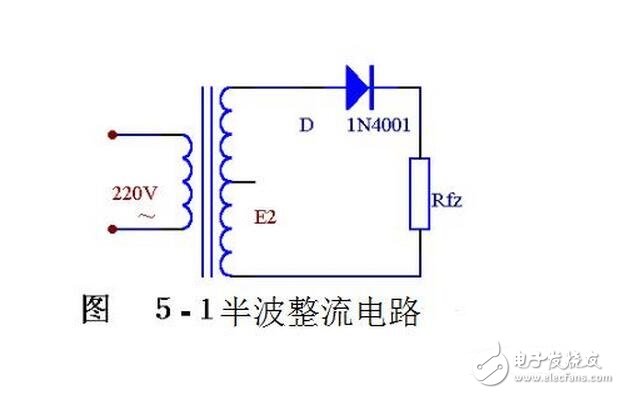
下面从图5-2的波形图上看着二极管是怎样整流的。图5-1、是一种最简单的整流电路。它由电源变压器B 、整流二极管D 和负载电阻Rfz ,组成。变压器把市电电压(多为220伏)变换为所需要的交变电压e2,D 再把交流电变换为脉动直流电。
变压器砍级电压e2,是一个方向和大小都随时间变化的正弦波电压,它的波形如图5-2(a)所示。在0~K时间内,e2为正半周即变压器上端为正下端为负。此时二极管承受正向电压面导通,e2通过它加在负载电阻Rfz上,在~2 时间内,e2为负半周,变压器次级下端为正,上端为负。这时D承受反向电压,不导通,Rfz,上无电压。在~2时间内,重复0~ 时间的过程,而在3~4时间内,又重复~2时间的过程这样反复下去,交流电的负半周就被“削”掉了,只有正半周通过Rfz,在Rfz上获得了一个单一右向(上正下负)的电压,如图5-2(b)所示,达到了整流的目的,但是,负载电压Usc。以及负载电流的大小还随时间而变化,因此,通常称它为脉动直流。
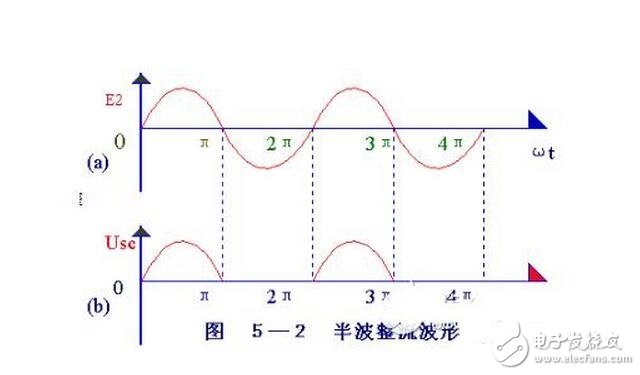
这种除去半周、图下半周的整流方法,叫半波整流。不难看出,半波整说是以“牺牲”一半交流为代价而换取整流效果的,电流利用率很低(计算表明,整流得出的半波电压在整个周期内的平均值,即负载上的直流电压Usc =0.45e2 )因此常用在高电压、小电流的场合,而在一般无线电装置中很少采用。
如果把整流电路的结构作一些调整,能够获得一种能充分的利用电能的全波整流电路。图5-3 是全波整流电路的电原理图。
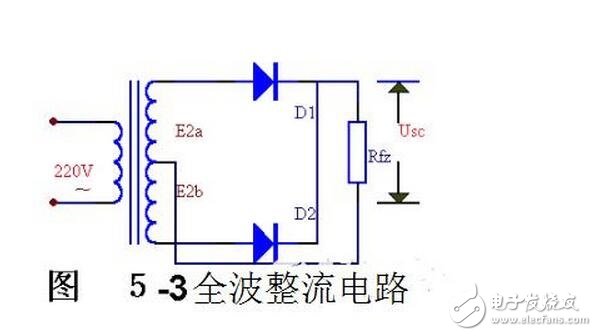
全波整流电路,可以看作是由两个半波整流电路组合成的。变压器次级线圈中间需要引出一个抽头,把次组线圈分成两个对称的绕组,从而引出大小相等但极性相反的两个电压e2a 、e2b ,构成e2a 、D1、Rfz与e2b 、D2、Rfz ,两个通电回路。
全波整流电路的工作原理,可用图5-4 所示的波形图说明。在0~间内,e2a 对Dl为正向电压,D1导通,在Rfz 上得到上正下负的电压;e2b 对D2为反向电压,D2 不导通(见图5-4(b)。在-2时间内,e2b 对D2为正向电压,D2导通,在Rfz 上得到的仍然是上正下负的电压;e2a 对D1为反向电压,D1 不导通(见图5-4(C)。
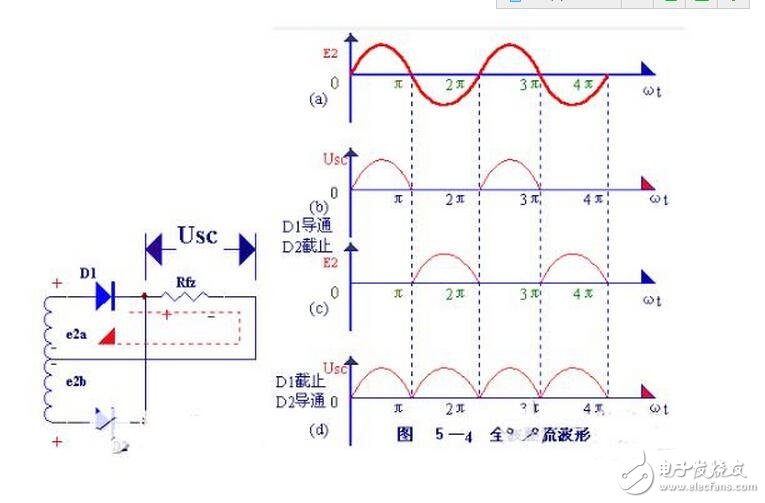
如此反复,由于两个整流元件D1、D2轮流导电,结果负载电阻Rfz 上在正、负两个半周作用期间,都有同一方向的电流通过,如图5-4(b)所示的那样,因此称为全波整流,全波整流不仅利用了正半周,而且还巧妙地利用了负半周,从而大大地提高了整流效率(Usc=0.9e2,比半波整流时大一倍)。
图5-3所示的全波整滤电路,需要变压器有一个使两端对称的次级中心抽头,这给制作上带来很多的麻烦。另外,这种电路中,每只整流二极管承受的最大反向电压,是变压器次级电压最大值的两倍,因此需用能承受较高电压的二极管。
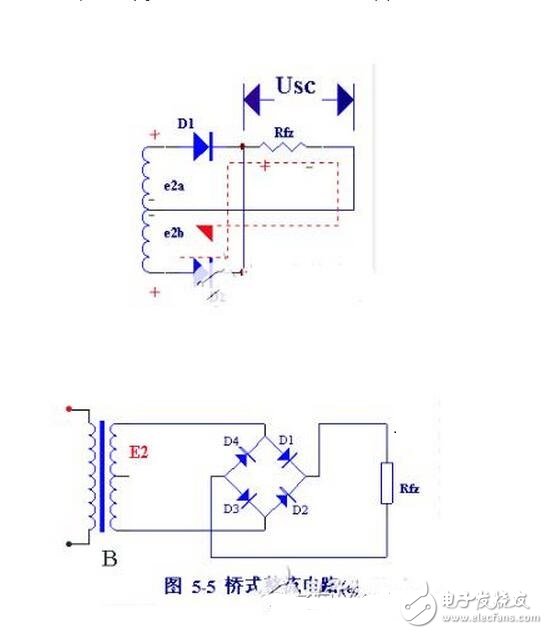
桥式整流电路是使用最多的一种整流电路。这种电路,只要增加两只二极管口连接成“桥”式结构,便具有全波整流电路的优点,而同时在某些特定的程度上克服了它的缺点。
桥式整流电路的工作原理如下:e2为正半周时,对D1、D3和方向电压,Dl,D3导通;对D2、D4加反向电压,D2、D4截止。电路中构成e2、Dl、Rfz 、D3通电回路,在Rfz ,上形成上正下负的半波整洗电压,e2为负半周时,对D2、D4加正向电压,D2、D4导通;对D1、D3加反向电压,D1、D3截止。电路中构成e2、D2Rfz 、D4通电回路,同样在Rfz 上形成上正下负的另外半波的整流电压。
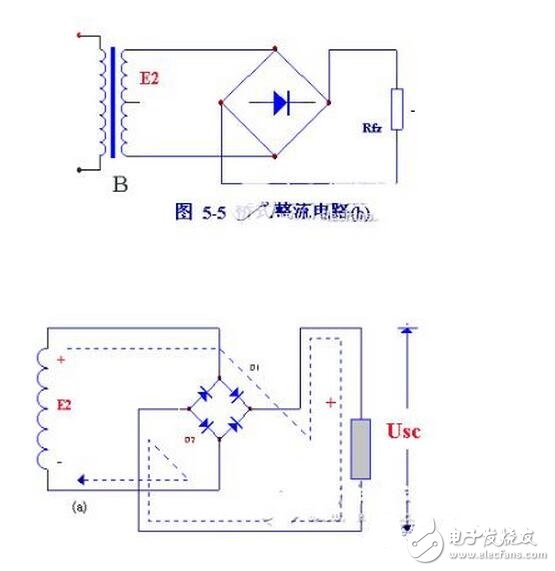
如此重复下去,结果在Rfz ,上便得到全波整流电压。其波形图和全波整流波形图是一样的。从图5-6中还显而易见,桥式电路中每只二极管承受的反向电压等于变压器次级电压的最大值,比全波整洗电路小一半!
需要特别指出的是,二极管作为整流元件,要根据不同的整流方式和负载大小加以选择。。如选择不当,则或者不能安全工作,甚至烧了管子;或者大材小用,造成浪费。表5-1 所列参数可供选择二极管时参考。
“另外,在高电压或大电流的情况下,如果手头没有承受高电压或整定大电滤的整流元件,可以把二极管串联或并联起来使用。
图5-7 示出了二极管并联的情况:两只二极管并联、每只分担电路总电流的一半口三只二极管并联,每只分担电路总电流的三分之一。总之,有几只二极管并联,”流经每只二极管的电流就等于总电流的几分之一。但是,在实际并联运用时“,由于各二极管特性不完全一致,不能均分所通过的电流,会使有的管子困负担过重而烧毁。因此需在每只二极管上串联一只阻值相同的小电阻器,使各并联二极管流过的电流接近一致。这种均流电阻R一般都会采用零点几欧至几十欧的电阻器。电流越大,R应选得越小。
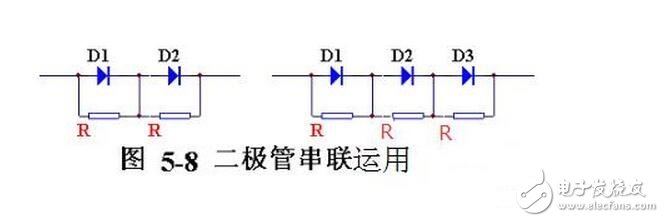
图5-8示出了二极管串联的情况。显然在理想条件下,有几只管子串联,每只管子承受的反向电压就应等于总电压的几分之一。但因为每只二极管的反向电阻不完全一样,会造成电压分配不均:内阻大的二极管,有可能由于电压过高而被击穿,并由此引起连锁反应,逐个把二极管击穿。在二极管上并联的电阻R,可以使电压分配均匀。均压电阻要取阻值比二极管反向电阻值小的电阻器,各个电阻器的阻值要相等。向电阻值小的电阻器,各个电阻器的阻值要相等。
某一电压(或电流)的有效值与其平均值之比,我们叫做波形系数。在可控硅整流电路中波形系数是个有必要注意一下的问题。为说明这样的一个问题,我们先按图1所示的可控硅半波整流电路做个实验,各元件的型号和参数仅供参考。
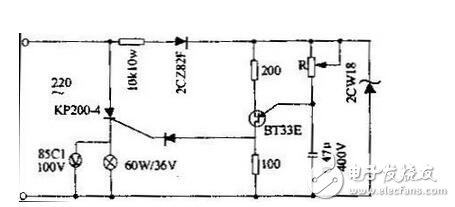
先将R值调至最大,接通电源,此时直流电压表指示为零,灯泡不亮。然后慢慢减小R值,电压表读数逐渐增大,灯泡逐渐增亮。我们会发现当直流电压表指示为10伏时,灯泡便达到正常亮度了,这就是说灯泡的功耗已达额定功率了,若再继续增高电压,灯泡就可能烧毁。为什么电压表的读数还远未达到灯泡的额定电压36伏,而灯泡的功耗却已达到额定功率了呢?
灯光中流过的电流是单向脉动电流,灯泡两端的电压为单向脉动电压,其波形如图2中实线所示。直流电压表的读数是这种脉动电压的平均值,而刁;是它的有效值。其有效值却要比平均值大得多。
根据电工学知识,这种周期性的单向脉动电压的有效值U。乃是瞬时值的平方在一个周期内平均值的算术平方根(均方根值),即

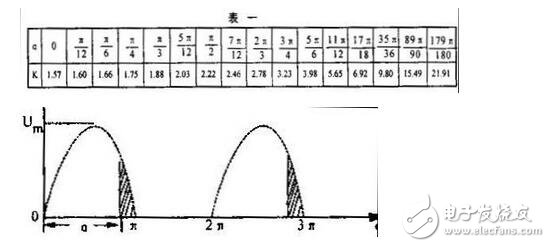
将不同的Q值代入式(3),就得到相应的K值,如表一所示。由表一能够准确的看出,当可控硅的移相角由零变到n时,波形系数K值逐渐增大,而且增大的速度慢慢的变快,当。接近,I时,K值将急聚增加(而U和Uo都急聚下降。)
现在再来看看实验结果。据式(2)可算出,当直流电压表指示10伏即U。=10伏时,CO$n=-0.7979,波形系数K~3.57, Uo~35.7伏。Uo己相当接近灯泡的额定电压了,所以灯泡达到正常亮度。
根据同样的道理可算出, 当G相同时,在电阻性负载的全波可控整流电路中,输出脉动电压(波形见图3中的实线倍。在上述计算中,均忽略了可控硅导通时的正向压降。对别的形式的整流电路以及负载呈电感性时输出电压的波形系数,本文不再赘述。
由上面的分析可知,在用可控硅进一行整流时,直流电压表(或电流表)上L的读数是输出电压(或电流)的平均1K值,不能将读数直接代入公式卜U2 L来计算负载上的功耗,是因为式中U为负载R,上的电压有效值,即U=Uo。
(1) 尽量减小可控硅的移相角,如Q:o时,则K=I.57(单相半波): (2)当负载标称电压比输入交流电压的有效值低得多时,先用变压器降压再进行整流; (3)尽量采用单向可控整流或三相可控整流电路。如忽视波形系数的影响,尽管电压表的读数还远未达到负载的额定电压,但仍有可能烧毁电器,以致造成不应有的损失。这是一定要注意的。
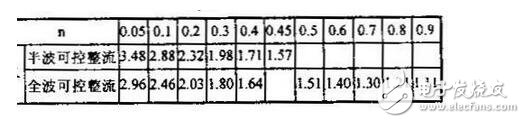
在实际应用中,为方便起见,我们可根据表二来估算不同的输出直流电压时的波形系数,从而估算出输出电压的有效值。表二中的n为直流电压表的读数U。与输入交流电压有效值U的比。即 23 (3),便可得到相应的波形系数K。例如在图1所示的电路中,当直流电压表指示为 50伏时,n=50/220~0.23,根据表二可估算出此时波形系数K在2.32和1.98之间。
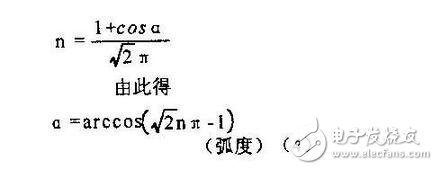
根据同样的道理,可得出全波可控整流电路中,对应于不同n值(可控硅全导通时n取得最大值0.9)时的波形系数K